El plano cartesiano.
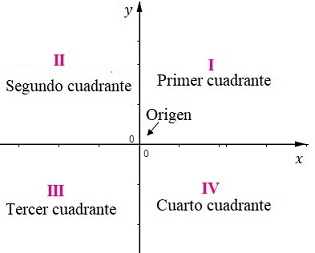
El plano cartesiano es un sistema coordenado rectangular (que forma un rectángulo), formado por dos rectas numéricas que se intersecan perpendicularmente en un punto llamado origen, correspondiente al punto cero de cada una de las rectas, mediante un sistema de coordenadas.
Las rectas numéricas horizontal y vertical son llamadas eje de abscisas (usualmente el eje \(x\)) y eje de ordenadas (usualmente eje \(y\)).
El plano que queda determinado por los ejes recibe el nombre de plano \(xy\) y permite unir dos de las ramas más importante de las matemáticas, el álgebra y la geometría, las cuales siembran las bases para el estudio de otras ramas como son la trigonometría y el cálculo (se estudia en grados superiores).
Recuerde que una recta se extiende en ambos sentidos (derecha o izquierda, arriba o abajo) hasta el infinito, sin embargo, solo se debe colocar flechas de dirección hacia la derecha y hacia arriba. Las escalas de división se toman a conveniencia de acuerdo con los valores que toman las variables del ejercicio, esto es porque el tamaño de la hoja de papel o cartulina donde escribe es limitado y la escala debe acomodarse a los datos.
Coordenadas de un punto en el plano.
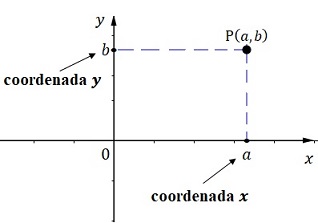
Sea \(P\) un punto en el plano cartesiano, ubicado en cualquiera de los cuadrantes. Se asocia un par ordenado (pareja de números reales que tienen un orden) al punto \(P\) si se traza una recta vertical desde \(P\) al eje de abscisas (eje \(x\) y una recta horizontal desde \(P\) al eje de ordenadas (eje \(y\)).
Si la recta vertical corta el eje de abscisas en \(x=a\) y la recta horizontal corta el eje de ordenada en \(y=b,\) el par ordenado de números reales asociado al punto \(P\) es \(\left(a,b\right).\) El número \(a\) es la abscisa o coordenada en \(x\) del punto y el número \(b\) es la ordenada o coordenada en \(y.\) Un punto en un plano también se puede representar por el par ordenado \(\left(x,y\right)\) o \(\left(h,k\right)\) las letras a usar no importan, lo que importa es el orden.
Graficar puntos en el plano de coordenadas.
Por convención se ha establecido que a la derecha y arriba del origen de coordenadas, punto \((0,0)\) es positivo, mientras que a la izquierda y abajo se considera negativo como puede verse en la figura de derecha.
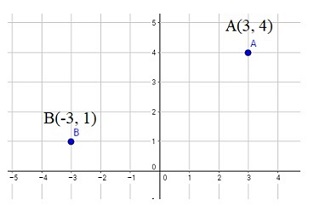
Así el punto \(\left(3,4\right)\) quiere decir tres unidades (lugares) a la derecha del \(\left(0,0\right)\) y luego cuatro unidades hacia arriba. Para el punto \(\left(-3,1\right)\) se deben considerar tres unidades a la izquierda del origen \(\left(0,0\right)\) y luego una unidad hacia arriba, como puede verse en la figura de la izquierda.
Distancia entre dos puntos en el plano.
Comience por entender la distancia entre dos números \( n_1\) y \( n_2\) en la recta real, esta se define como el valor absoluto de la diferencia de esto, es decir \(d(n_1, n_2)=|n_2- n_1 |\).
Ejemplo 1. Determinar la distancia entre \(-20\) y \(15.\) $$d(15,-20)=|-20-15|=|-35|=35$$ Ahora considere lo que pasa en el plano. Se define la distancia entre dos puntos en el plano \(A(x_1, y_1)\) y \(B(x_2, y_2)\) como el valor numérico (valor absoluto) de la longitud del segmento rectilíneo que une esos dos puntos. A continuación, se presenta deducción de la expresión para la determinación de la distancia entre dos puntos en el plano.
Deducción de la fórmula de la distancia entre dos puntos.
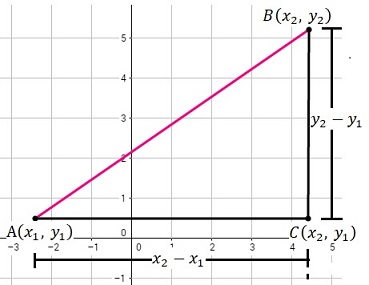 En la figura de la izquierda note que si desea ir desde el punto A hasta B puede hacerlo siguiendo dos caminos diferentes, el camino de color rosa, o el camino de color negro pasando por C. Como puede notar el camino de color rosa es una línea recta, y según el teorema de Pitágoras es la distancia más corta desde A hasta B y por tanto la distancia entre ellos.
Para determinar el valor de la distancia \(d\) entre \(A\) y \(B\) se emplea el teorema de Pitágoras donde \(d\) es la hipotenusa del triángulo rectángulo y además \(d(A,B )=d(B,A).\)
En la figura de la izquierda note que si desea ir desde el punto A hasta B puede hacerlo siguiendo dos caminos diferentes, el camino de color rosa, o el camino de color negro pasando por C. Como puede notar el camino de color rosa es una línea recta, y según el teorema de Pitágoras es la distancia más corta desde A hasta B y por tanto la distancia entre ellos.
Para determinar el valor de la distancia \(d\) entre \(A\) y \(B\) se emplea el teorema de Pitágoras donde \(d\) es la hipotenusa del triángulo rectángulo y además \(d(A,B )=d(B,A).\)
Distancia entre dos puntos en el plano.
$$d=\sqrt{(x_2-x_1 )^2+(y_2-y_1 )^2}$$
Ejemplo 2. Dados \(A(-3,2)\) y \(B(5,-4)\) determinar es la longitud del segmento \(\overline{AB}\)
Solución: la longitud de \(\overline{AB}\) está dada por \(d(A,B)\)
\begin{align}
&d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2)}\\
&d(A,B)=\sqrt{(5-(-3))^2+(-4-2)^2}\\
&d(A,B)=\sqrt{(64+36)}=\sqrt{100}=10\end{align}
Ejemplo 3. Dados \(A(6,3)\) y \(B(5,-2)\) determinar la longitud de \(\overline{AB}\)
Solución:
\begin{align}
&d(A,B)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\
&d(A,B)=\sqrt{(5-6)^2+(-2-3)^2)}\\
&d(A,B)=\sqrt{(-1)^2+(-5)^2}\\
&d(A,B)=\sqrt{1+25}=\sqrt{26}\end{align}
Note que \(\sqrt{26}\) no es una raíz exacta ni reducible, por tanto el resultado se deja expresado en radical.
Coordenadas del punto medio de un segmento.
Sean los puntos \(A(x_1,y_1)\) y \(B(x_2,y_2)\) dos puntos cualesquiera en el plano, los cuales determinan el segmento de recta \(\overline{AB}\). Las coordenadas del punto medio entre dichos puntos están dadas por la expresión matemática:
Coordenadas de punto medio
$$P_m=\left(\frac{x_1+x_2}2,\frac{y_1+y_2}2\right)$$
Ejemplo. Determinar las coordenadas del punto medio de AB en cada caso:
$$1.~~ A(-3,5),~~B(6,2)~~~~~~~2.~~ A(6,2),~~B(7,2)~~~~~~3. A(-3,3), B(5,7).$$
Solución: usando la fórmula para el punto medio se tiene,
\begin{align}
P_m (A,B)&=\left(\frac{-3+6}2,\frac{2+5}2\right)=\left(\frac32,\frac72\right)\\
P_m(A,B)&=\left(\frac{6+7}2,\frac{2+2}2\right)=\left(\frac{13}2,2\right)\\
P_m(A,B)&=\left(\frac{-3+5}2,\frac{3+7}2\right)=\left(1,5\right)
\end{align}
Para más contenidos y luego clic en la pestaña del contenido deseado.
División de un segmento en una razón dada.
Algunas veces se desea conocer las coordenadas de un punto \(P(x,\ y)\) que está a una razón dada de la distancia dirigida (importa el orden) entre dos puntos \(A(x_1,\ y_1)\) y \(B(x_2,\ y_2).\) Para tales fines las coordenadas del punto \(P(x,\ y)\) que divide la distancia d(A,B) en una razón dada están dada por: $$P(x,\ y)=\ P\left(\frac{x_1+rx_2}{1+r},\frac{y_1+ry_2}{1+r}\right)$$ donde \(r\) es la razón que en que se desea sea dividido el segmento, tal que, $$r=\frac{d(A,P)}{d(B,P)}=\frac{\overline{AP}}{\overline{BP}}$$
Ejemplo. Determinar las coordenadas del punto que está a los \(3/5\) de la distancia de \(C(5, 3)\) a \(D(-3, -2)\) sobre el segmento que los une.
Solución: sea el punto \(P(x,\ y)\) el punto cumple las condiciones planteadas, por tanto \(P(x,\ y)\) está a \(\frac{2d(C,D)}{5}\) del punto \(D\) (por ser \(\frac{3d}{5}+\frac{2d}{5}=d)\) de donde los puntos \(D,\ P\) y \(C\) son consecutivos en el segmento de recta que va desde \(C(5,\ 3)\) a \(D\left(-3,\ -2\right).\)
$$P(x,\ y)=\left(\frac{x_1+rx_2}{1+r},\frac{y_1+ry_2}{1+r}\right)$$
Determinando la razón \(r\) de proporción:
$$r=\frac{\overline{DP}}{\overline{PC}}\Longrightarrow r=\frac{\frac{3}{5}d(C,D)}{\frac{2}{5}d(C,D)}=\frac{3}{2}$$
Determinando las coordenadas de \(P\left(x,\ y\right):\)
\begin{align}
&P(x,\ y)=\left(\frac{5+\frac{3}{2}\left(-3\right)}{1+\frac{3}{2}},\ \frac{3+\frac{3}{2}\left(-2\right)}{1+\frac{3}{2}}\right)\\
&P(x,\ y)=\left(\frac{5+\frac{-9}{2}}{\frac{5}{2}},\ \frac{3+\left(-3\right)}{\frac{5}{2}}\right)\\
&P(x,\ y)=\left(\frac{\frac{1}{2}}{\frac{5}{2}},\ \frac{0}{\frac{5}{2}}\right)\\
&P(x,\ y)=\left(\frac{1}{5},0\right)\end{align}
Para saber más: se pude comprobarse que el punto \(P\left(\frac{1}{5},0\right)\) cumple con las condiciones de la situación, de la manera siguiente:
1. Distancia entre los puntos \(C\) y \(D.\)
\begin{align}
&d(C,D)=\sqrt{{(-3-5)}^2+{(-2-3)}^2}\\
&d(C,D)=\sqrt{64+25}=\sqrt{89}\end{align}
2. \(d(C,P)\) debe ser \(3/5\) de \(d(C,D)\)
\begin{align}
&d(C,P)=\sqrt{\left(5-\frac{1}{5}\right)^{2\ }+{(3-0)}^2}\\
&d(C,P)=\sqrt{\left(\frac{24}{5}\right)^{2\ }+3^2}\\
&d(C,P)=\sqrt{\frac{576}{25}+9}=\sqrt{\frac{801}{25}}\\
&d(C,P)=\frac{3\sqrt{89}}{5}\end{align}
3. \(d(P,D)\) debe ser \(2/5\) de \(d(C,D)\)
\begin{align}
&d(D,P)=\sqrt{\left(-3-\frac{1}{5}\right)^2+{(-2-0)}^2}\\
&d(D,P)=\sqrt{\left(\frac{-16}{5}\right)^2+{(-2)}^2}\\
&d(D,P)=\sqrt{\frac{356}{25}}=\frac{2\sqrt{89}}{5}\end{align}
4. Los puntos deben estar sobre un mismo segmento, como muesta la figura.
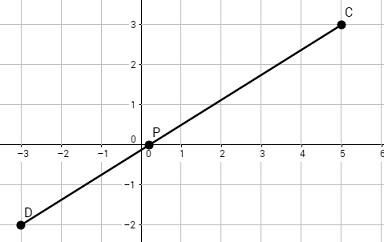
Para más contenidos y luego clic en la pestaña del contenido deseado.
Distancia de un punto a una recta.
En algunos casos se hace necesario determinar la distancia entre un punto \(P(x_1,y_1)\) y una recta \(ax+by+c=0.\) Mediante geometría euclidiana o análisis vectorial se puede demostrar que dicha distancia está dada por la expresión:
Distancia punto-recta
$$d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$$
Ejemplo 1. Determinar la distancia entre \(4x+3y-12=0\) y el punto \((1,1).\)
Solución:
\begin{align}
d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}
\end{align}
Donde el punto \(P(x_1,y_1)=(1,1)\) y comparando la recta \(4x+3y-12=0\) con \(ax+by+c=0\) entonces \(a=4;~ b=3;~ c=-12\) de donde realizando ahora el valor numérico para estos valores.
$$d=\frac{|4(1)+3(1)-12|}{\sqrt{4^2+3^2}}\Longrightarrow d=\frac{|4+3-12|}{\sqrt{25}}=\frac55=1$$
Ejemplo 2. Un punto sobre una recta. Determinar la distantica del punto \(P(-3,0)\) a la recta \(4x-5y=-12\)
Solución: \begin{align} d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}} \end{align} Al escribir la recta en forma general como \(4x-5y+12=0\) se tienen los valores \(a=4, b=-5, c=12\) y el punto \(P(x_1,y_1)=(-3,0)\) lo da el ejercicio, de donde, $$d=\frac{|4(-3)-5(0)+12|}{\sqrt{4^2+(-5)^2}}=\frac{0}{\sqrt{41}}=0$$ por tanto, el punto está sobre la recta (pertenece a ella).
Para más contenidos y luego clic en la pestaña del contenido deseado.
Perímetro de un triángulo. Grafique en el plano \(xy\) los puntos \(A(3,4),\) \(B(6, 8),\) y \(C(-2,4)\) luego una dos a dos con una línea los puntos y determine la longitud del contorno de la figura.
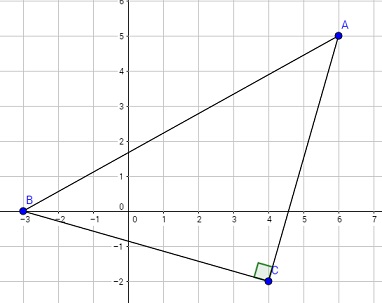
Triángulo rectángulo Justificar que los puntos \(A(6,5), B(-3,0)\) y \(C(4,-2)\) son los vértices de un triángulo rectángulo.
Medianas de un triángulo. Una mediana de un triángulo es el segmento de recta trazado desde el punto medio de uno de los lados hasta el vértice opuesto. Determine la longitud de las medianas del triángulo, cuyos vértices son \(A(3,2),B(-2,4),\) y \(C(-1,-1)\)
Perímetro y área. Los puntos \(A\left(3,5\right),B\left(8,5\right),C\left(-2,1\right)\) y \(D(3,1)\) son los vértices de un cuadrilátero. Determine el perímetro la figura y el área de la figura formada al unir los puntos de forma sucesiva.
Un triángulo rectángulo isósceles. Demostrar que \(A(-5, 3), B(3, 2)\) y \(C(-1, -4)\) son los vértices de un triángulo rectángulo isósceles.
Determinar los puntos de intersección con los ejes cartesianos y la forma simétrica de la recta \(4x-2y-10=0.\)
Verificar si los puntos \(A(6,5),~~B(-3,0)\) y \(C(4,-2)\) son los vértices de un triángulo rectángulo isósceles.

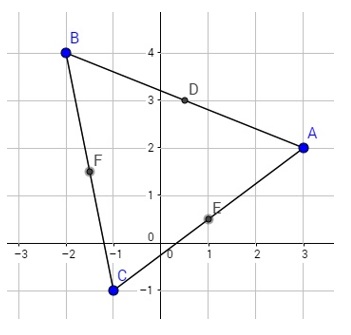 Como puede ver en el triángulo el punto \((1/2,3)\) está en lado opuesto al punto \(C(-1,-1),\) el punto \((1, 1/2)\) está en lado opuesto al punto \(B(-2,4)\) y el punto \((-3/2,3/2)\) está en lado opuesto al punto \(A(3,2).\)
Como puede ver en el triángulo el punto \((1/2,3)\) está en lado opuesto al punto \(C(-1,-1),\) el punto \((1, 1/2)\) está en lado opuesto al punto \(B(-2,4)\) y el punto \((-3/2,3/2)\) está en lado opuesto al punto \(A(3,2).\)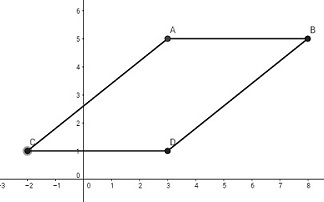 Solución: de la figura el perímetro \(p=l_1+l_2+l_3+l_4\) (longitudes de los lados) dadas por
Solución: de la figura el perímetro \(p=l_1+l_2+l_3+l_4\) (longitudes de los lados) dadas por